删数问题的贪心和动规解法
1.问题描述
现有一个n位数,你需要删除其中的k位,请问如何删除才能使得剩下的数最大?
比如当数为2319274 k=1时,删去2变成319274后是可能的最大值。
2.问题分析
[1]贪心解法
这题可以使用贪心策略,每次从高位向低位数,删除高位比低位数字小的那位上的数字,直到删除了k位之后,得到的数字肯定是最大值。
(1)删数问题具有最优子结构:
假设 $$a=x_{1}10^{n-1}+x_{2}10^{n-2}+ ··· +x_{p}10^{n-p}+x_{q}10^{n-q}+x_{r}10^{n-r} ··· +x_{n}$$ 有$$x_{q}<x_{r}$$,即要删除$$x_{q}$$则有: $$a_{1}=x_{1}10^{n-2}+x_{2}10^{n-3}+ ··· +x_{p}10^{n-p-1}+x_{r}10^{n-r} ··· +x_{n}$$ 假设删去的不是$$x_{q}$$,而是其它位,则有: $$a_{2}=x_{1}10^{n-2}+x_{2}10^{n-3}+ ··· +x_{p}10^{n-p-1}+x_{q}10^{n-q} ··· +x_{n}$$ 由于$$x_{1}>x_{2}>···>x_{p}>x_{q}$$且$$x_{q}<x_{r}$$,则有$$a_{1}>a_{2}$$。 因此,删数问题满足最优子结构性质。
(2)删数问题具有贪心选择性质:
设问题T已按照上面的方法删除,假设 $$A=(y_{1},y_{2}, ···,y_{k})$$ 是删数问题的一个最优解。易知,若问题有解,则$1≤ k ≤ n$。 (1)当k=1时,由前得证,$$A=(y_{1},A’)$$是问题的最优解,其中$A’$是$A$中不删除了$$y_{1}$$而删除其他位的最优解; (2)当k=q时,由反证法,可得$$A=(y_{1},y_{2} ··· ,y_{q})$$是最优解; 当k=q+1时,由前得证,$$A=(y_{1},y_{2} ··· ,y_{q}+ y_{q}+1)$$是最优解。 所以,删数问题具有贪心选择性质。
代码很容易实现,AC,1.484s,1.089MB
#include <string>
#include <iostream>
using namespace std;
int t,k,len;
string name;
void deletek(){
int tlen=name.length();
int tk=k;
bool flag=true;
while (k--> 0 && flag) {
flag=false;
len = name.length();
for (int i=0; i<len; i++) {
if (i+1<len && name[i]<name[i+1]) {
name.erase(i,1);
len--;
flag=true;
break;
}
}
}
cout << name.substr(0,tlen-tk) << endl;
}
int main(int argc, const char * argv[])
{
cin >> t;
while (t-->0) {
cin >> name;
cin >> k;
deletek();
}
return 0;
}
[2]动态规划解法
根据上面的分析可以看出此题还可用动态规划来解决,思路如下:
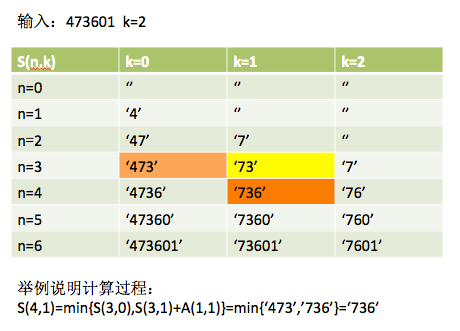
假设$A(i,j)$表示输入数字(字符串)的从第i位到第j位数字组成的字符串,$S(i,j)$表示前i位中删除j位得到的最优解,它实际上可以看做两个子问题:如果删除第j位,那么$S(i,j)$等于前i-1位删除j-1位的最优解加上第j位数字;如果不删除第j位,那么$S(i,j)$等于前i-1位删除j位的最优解。于是便有下面的递推式:
$$ S(i,j)= \left{ \begin{array}{l l} A(0,i) & \quad \text{此时j=0}\ min({S(i-1,j-1),S(i-1,j)+A(j,j)}) & \quad \text{此时0<j<i} \end{array} \right. $$
这个递推式非常类似最长公共子序列问题的递推式,所以解法也类似,在空间方面可以只使用一个一维数组,加上一个额外的O(1)的空间,计算过程如下面制作的表格所示,除了第一列,其他中间元素都只依赖于上面一行对应位置$S(i-1,j)$和上面一行左边位置$S(i-1,j-1)$两个元素的大小,比较的是字符串,使用字典序进行比较,C++内置的字符串比较函数compare即可。
动态规划实现代码 [这份代码没有AC,只能得到60分就超时了,应该还可以改进]
#include <string>
#include <iostream>
using namespace std;
#define MAX_K 1001
int t,k;
string name;string up;string last;string temp;
void deletek(){
int len=name.length();
if(k>=len){
cout << "" << endl;
return;
}
string cur[MAX_K]={""};
for (int i=1; i <= len; i++) {
for (int j=0; j < i && j <= k; j++) {//
if (j==0) {//sub string
last=cur[j];
cur[j]=name.substr(0,i);
}else{//0 < j <= i
up=cur[j]+name[i-1];//
if (up.compare(last)>=0) {//up > left
last=cur[j];
cur[j]=up;
}else{//up < left
temp=cur[j];
cur[j]=last;
last=temp;
}
}
}
}
cout << cur[k] << endl;
}
int main(int argc, const char * argv[])
{
cin >> t;
while (t-->0) {
cin >> name;
cin >> k;
deletek();
}
return 0;
}
从这道题中可以看出,虽然动态规划每次做出当前情况下最好的决策,但是为了做出最好的决策花费了大量的时间和空间,对于删数问题贪心算法应该是较好的解决方案。