Python数据结构篇(3) 数据结构
参考内容:
1.Problem Solving with Python
Chapter 2 Algorithm Analysis
Chapter 3 Basic Data Structures
Chapter 6 Trees and Tree Algorithms
2.算法导论
数据结构总结
1.Python内置数据结构的性能分析
(1)List
List的各个操作的时间复杂度

同样是执行1000次创建一个包含1-1000的列表,四种方式使用的时间差距很大!使用append比逐次增加要快很多,另外,使用python的列表产生式比append要快,而第四种方式更加快!
def test1():
l = []
for i in range(1000):
l = l + [i]
def test2():
l = []
for i in range(1000):
l.append(i)
def test3():
l = [i for i in range(1000)]
def test4():
l = list(range(1000))
# Import the timeit module -> import timeit
# Import the Timer class defined in the module
from timeit import Timer
# If the above line is excluded, you need to replace Timer with
# timeit.Timer when defining a Timer object
t1 = Timer("test1()", "from __main__ import test1")
print("concat ",t1.timeit(number=1000), "milliseconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "milliseconds")
t3 = Timer("test3()", "from __main__ import test3")
print("comprehension ",t3.timeit(number=1000), "milliseconds")
t4 = Timer("test4()", "from __main__ import test4")
print("list range ",t4.timeit(number=1000), "milliseconds")
# ('concat ', 1.7890608310699463, 'milliseconds')
# ('append ', 0.13796091079711914, 'milliseconds')
# ('comprehension ', 0.05671119689941406, 'milliseconds')
# ('list range ', 0.014147043228149414, 'milliseconds')
测试pop操作:从结果可以看出,pop最后一个元素的效率远远高于pop第一个元素
x = list(range(2000000))
pop_zero = Timer("x.pop(0)","from __main__ import x")
print("pop_zero ",pop_zero.timeit(number=1000), "milliseconds")
x = list(range(2000000))
pop_end = Timer("x.pop()","from __main__ import x")
print("pop_end ",pop_end.timeit(number=1000), "milliseconds")
# ('pop_zero ', 1.9101738929748535, 'milliseconds')
# ('pop_end ', 0.00023603439331054688, 'milliseconds')
还有一个有意思的对比是list的append(value)和insert(0, value),即一个从后面插入(后插),另一个从前面插入(前插),前者的效率远远高于后者。
Python的list的实现不是类似数据结构中的单链表,而是类似数组,也就是说list中的元素保存在一片连续的内存区域中,这样的话只有知道元素索引就能确定元素的内存位置,从而直接取出该位置上的值,但是它的缺点在于前插需要移动元素,而且随着list中元素的增多需要移动的元素也就越多,花费的时间也就自然多了。而单链表不同,单链表要得到某个位置上的元素必须要从头开始遍历,但是它的插入操作(前插或者后插)基本上都是恒定的时间,与链表中元素的多少没有关系,因为元素之间用“指针”维护着他们的关系。
个人认为,Python的list其实是动态表,类似C++中的vector等或者Java中的ArrayList等,在算法导论的平摊分析章节的最后,详细讲解了动态表的扩张和收缩,根据装载因子的取值大小,当它高于某个固定值(例如$\frac{1}{2}$)时扩张表,当它低于某个固定值(例如$\frac{1}{4}$)时收缩表,这样就能保证表的利用率达到一个满意的程度(例如50%以上的位置都是有元素的),感兴趣可以阅读原书。
(2)Dictionary
Dictionary的各个操作的性能

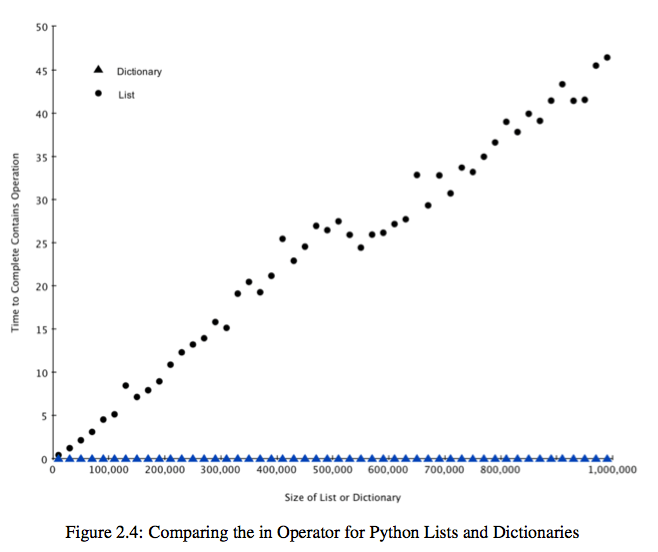
Dictionary和List的性能比较:list基本上随着其元素的数目呈线性增长,而dictionary一直维持在很短很短的时间内(我的机子测试的结果都是0.001ms)。Dictionary类似Java中的HashMap,内部实现使用了前面提到的hash函数,所以查找和删除都是常数时间的。
import timeit
import random
for i in range(10000,1000001,20000):
t = timeit.Timer("random.randrange(%d) in x"%i,"from __main__ import random,x")
x = list(range(i))
lst_time = t.timeit(number=1000)
x = {j:None for j in range(i)}
d_time = t.timeit(number=1000)
print("%d,%10.3f,%10.3f" % (i, lst_time, d_time))
结果图
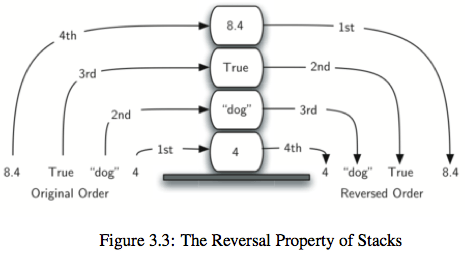
2.栈:LIFO结构,后进先出
栈能解决的问题很多,比如逆波兰表达式求值,求一个十进制数的二进制表达,检查括号匹配问题以及图的深度搜索等等,都很简单,可查看参考内容1学习。
# Completed implementation of a stack ADT
class Stack:
def __init__(self):
self.items = []
def is_empty(self):
return self.items == []
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
s = Stack()
print(s.is_empty())
s.push(4)
s.push('dog')
print(s.peek())
s.push(True)
print(s.size())
print(s.is_empty())
s.push(8.4)
print(s.pop())
print(s.pop())
print(s.size())
3.队列:FIFO结构,先进先出
队列一般用于解决需要优先队列的问题或者进行广度优先搜索的问题,也很简单。
# Completed implementation of a queue ADT
class Queue:
def __init__(self):
self.items = []
def is_empty(self):
return self.items == []
def enqueue(self, item):
self.items.insert(0,item)
def dequeue(self):
return self.items.pop()
def size(self):
return len(self.items)
q = Queue()
q.enqueue('hello')
q.enqueue('dog')
print(q.items)
q.enqueue(3)
q.dequeue()
print(q.items)
4.双向队列:左右两边都可以插入和删除的队列
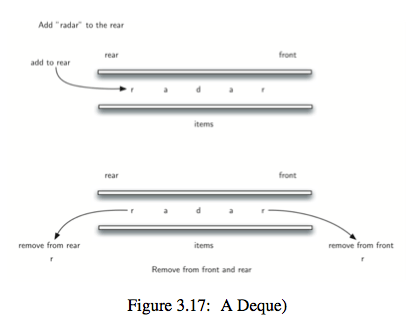
下面的实现是以右端为front,左端为rear
# Completed implementation of a deque ADT
class Deque:
def __init__(self):
self.items = []
def is_empty(self):
return self.items == []
def add_front(self, item):
self.items.append(item)
def add_rear(self, item):
self.items.insert(0,item)
def remove_front(self):
return self.items.pop()
def remove_rear(self):
return self.items.pop(0)
def size(self):
return len(self.items)
dq=Deque();
dq.add_front('dog');
dq.add_rear('cat');
print(dq.items)
dq.remove_front();
dq.add_front('pig');
print(dq.items)
5.二叉树:一个节点最多有两个孩子节点的树。如果是从0索引开始存储,那么对应于节点p的孩子节点是2p+1和2p+2两个节点,相反,节点p的父亲节点是(p-1)/2位置上的点
二叉树的应用很多,比如对算术表达式建立一颗二叉树可以清楚看出表达式是如何计算的(详情请见参考内容1),二叉树的变种可以得到其他的有一定特性的数据结构,例如后面的二叉堆。二叉树的三种遍历方法(前序,中序,后序)同样有很多的应用,比较简单,略过。
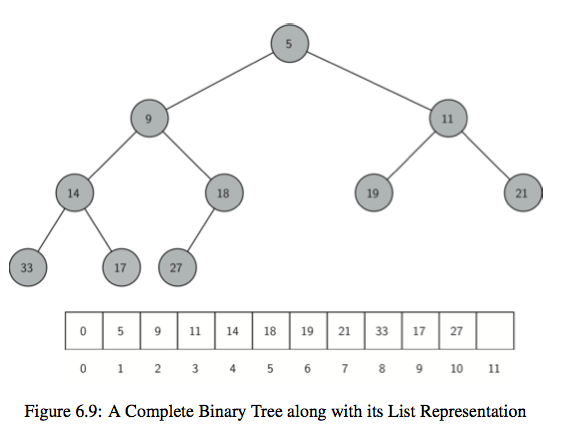
第一种,直接使用list来实现二叉树,可读性差
def binary_tree(r):
return [r, [], []]
def insert_left(root, new_branch):
t = root.pop(1)
if len(t) > 1:
#new_branch becomes the left node of root, and original left
#node t becomes left node of new_branch, right node is none
root.insert(1, [new_branch, t, []])
else:
root.insert(1, [new_branch, [], []])
return root
def insert_right(root, new_branch):
t = root.pop(2)
if len(t) > 1:
root.insert(2, [new_branch, [], t])
else:
root.insert(2, [new_branch, [], []])
return root
def get_root_val(root):
return root[0]
def set_root_val(root, new_val):
root[0] = new_val
def get_left_child(root):
return root[1]
def get_right_child(root):
return root[2]
r = binary_tree(3)
insert_left(r, 4)
insert_left(r, 5)
insert_right(r, 6)
insert_right(r, 7)
print(r)
l = get_left_child(r)
print(l)
set_root_val(l, 9)
print(r)
insert_left(l, 11)
print(r)
print(get_right_child(get_right_child(r)))
第二种,使用类的形式定义二叉树,可读性更好
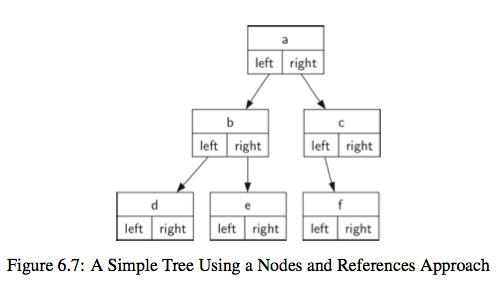
class BinaryTree:
def __init__(self, root):
self.key = root
self.left_child = None
self.right_child = None
def insert_left(self, new_node):
if self.left_child == None:
self.left_child = BinaryTree(new_node)
else:
t = BinaryTree(new_node)
t.left_child = self.left_child
self.left_child = t
def insert_right(self, new_node):
if self.right_child == None:
self.right_child = BinaryTree(new_node)
else:
t = BinaryTree(new_node)
t.right_child = self.right_child
self.right_child = t
def get_right_child(self):
return self.right_child
def get_left_child(self):
return self.left_child
def set_root_val(self, obj):
self.key = obj
def get_root_val(self):
return self.key
r = BinaryTree('a')
print(r.get_root_val())
print(r.get_left_child())
r.insert_left('b')
print(r.get_left_child())
print(r.get_left_child().get_root_val())
r.insert_right('c')
print(r.get_right_child())
print(r.get_right_child().get_root_val())
r.get_right_child().set_root_val('hello')
print(r.get_right_child().get_root_val())
6.二叉堆:根据堆的性质又可以分为最小堆和最大堆,是一种非常好的优先队列。在最小堆中孩子节点一定大于等于其父亲节点,最大堆反之。二叉堆实际上是一棵完全二叉树,并且满足堆的性质。对于插入和查找操作的时间复杂度度都是$O(logn)$。
它的插入操作图示:
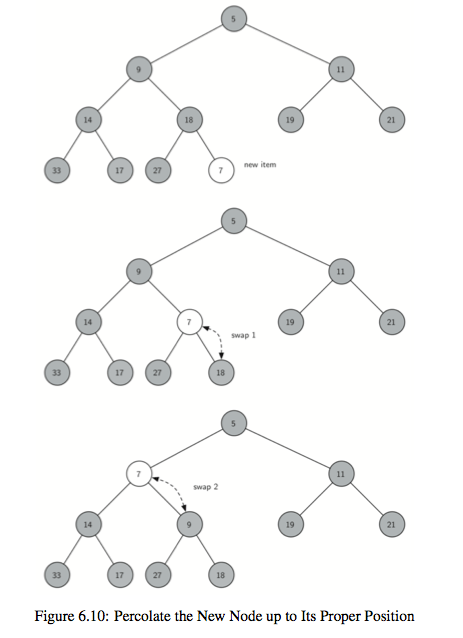
去除根节点的操作图示:
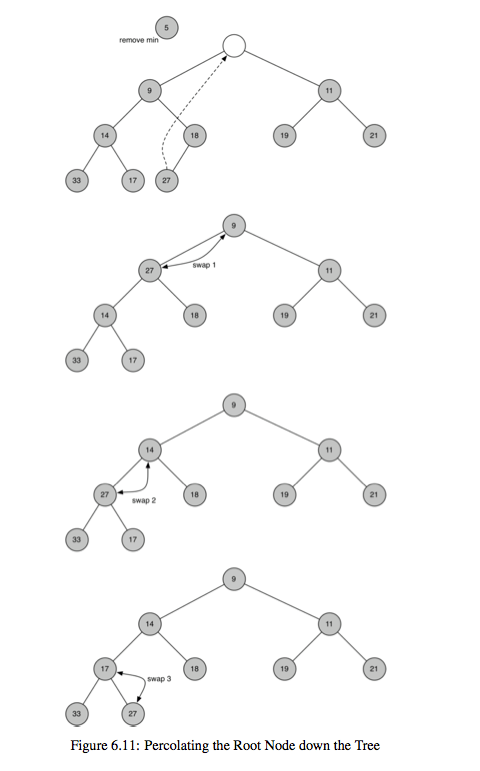
注意,下面的代码实现中默认在初始的堆列表中插入了一个元素0,这样做可以保证堆的真实有效的元素个数和current_size值对应,而且最后一个元素的索引就对应了current_size。
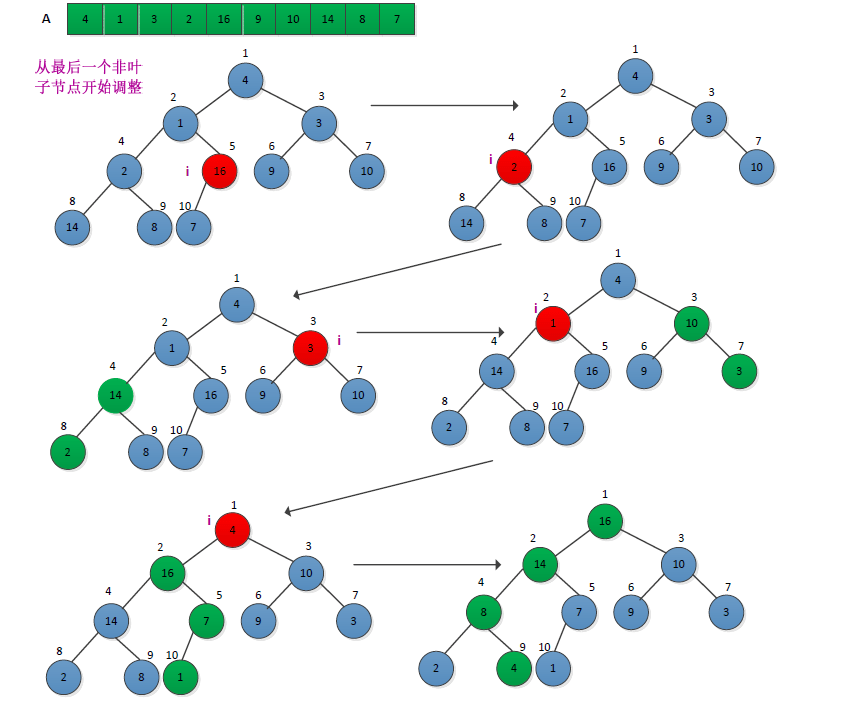
此外,从list中建堆的过程需要从最后一个非叶子节点开始到第一个非叶子节点(根节点)进行,这篇文章详细地解释了这个问题。建堆的过程如下:
[下图摘自原博客,版权归原作者,谢谢]
class BinHeap:
def __init__(self):
self.heap_list = [0]
self.current_size = 0
def perc_up(self, i):
while i // 2 > 0: # >0 means this node is still available
if self.heap_list[i] < self.heap_list[i // 2]:
tmp = self.heap_list[i // 2]
self.heap_list[i // 2] = self.heap_list[i]
self.heap_list[i] = tmp
i = i // 2
def insert(self, k):
self.heap_list.append(k)
self.current_size = self.current_size + 1
self.perc_up(self.current_size)
def perc_down(self, i):
while (i * 2) <= self.current_size:
mc = self.min_child(i)
if self.heap_list[i] > self.heap_list[mc]:
tmp = self.heap_list[i]
self.heap_list[i] = self.heap_list[mc]
self.heap_list[mc] = tmp
i = mc
def min_child(self, i):
if i * 2 + 1 > self.current_size:
return i * 2
else:
if self.heap_list[i * 2] < self.heap_list[i * 2 + 1]:
return i * 2
else:
return i * 2 + 1
def del_min(self):
ret_val = self.heap_list[1]
self.heap_list[1] = self.heap_list[self.current_size]
self.current_size = self.current_size - 1
self.heap_list.pop()
self.perc_down(1)
return ret_val
def build_heap(self, a_list):
i = len(a_list) // 2
self.current_size = len(a_list)
self.heap_list = [0] + a_list[:] #append original list
while (i > 0):
#build the heap we only need to deal the first part!
self.perc_down(i)
i=i-1
a_list=[9, 6, 5, 2, 3];
bh=BinHeap();
bh.build_heap(a_list);
print(bh.heap_list)
print(bh.current_size)
bh.insert(10)
bh.insert(7)
print(bh.heap_list)
bh.del_min();
print(bh.heap_list)
print(bh.current_size)
关于二叉查找树等内容请见树的总结。