Python数据结构篇(2) 排序
参考内容:
1.Problem Solving with Python
Chapter5: Search and Sorting online_link
2.算法导论
排序总结
1.冒泡排序(bubble sort):每个回合都从第一个元素开始和它后面的元素比较,如果比它后面的元素更大的话就交换,一直重复,直到这个元素到了它能到达的位置。每次遍历都将剩下的元素中最大的那个放到了序列的“最后”(除去了前面已经排好的那些元素)。注意检测是否已经完成了排序,如果已完成就可以退出了。时间复杂度$O(n^2)$
Python支持对两个数字同时进行交换!a,b = b,a就可以交换a和b的值了。

def short_bubble_sort(a_list):
exchanges = True
pass_num = len(a_list) - 1
while pass_num > 0 and exchanges:
exchanges = False
for i in range(pass_num):
if a_list[i] > a_list[i + 1]:
exchanges = True
a_list[i],a_list[i+1] = a_list[i+1], a_list[i]
pass_num = pass_num - 1
if __name__ == '__main__':
a_list=[20, 40, 30, 90, 50, 80, 70, 60, 110, 100]
short_bubble_sort(a_list)
print(a_list)
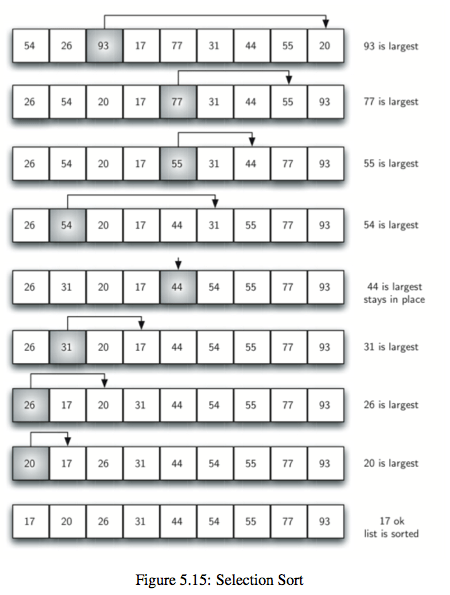
2.选择排序(selection sort):每个回合都选择出剩下的元素中最大的那个,选择的方法是首先默认第一元素是最大的,如果后面的元素比它大的话,那就更新剩下的最大的元素值,找到剩下元素中最大的之后将它放入到合适的位置就行了。和冒泡排序类似,只是找剩下的元素中最大的方式不同而已。时间复杂度$O(n^2)$
def selection_sort(a_list):
for fill_slot in range(len(a_list) - 1, 0, -1):
pos_of_max = 0
for location in range(1, fill_slot + 1):
if a_list[location] > a_list[pos_of_max]:
pos_of_max = location
a_list[fill_slot],a_list[pos_of_max]=a_list[pos_of_max],a_list[fill_slot]
a_list = [54, 26, 93, 17, 77, 31, 44, 55, 20]
selection_sort(a_list)
print(a_list)
3.插入排序(insertion sort):每次假设前面的元素都是已经排好序了的,然后将当前位置的元素插入到原来的序列中,为了尽快地查找合适的插入位置,可以使用二分查找。时间复杂度$O(n^2)$,别误以为二分查找可以降低它的复杂度,因为插入排序还需要移动元素的操作!

def insertion_sort(a_list):
for index in range(1, len(a_list)):
current_value = a_list[index]
position = index
while position > 0 and a_list[position - 1] > current_value:
a_list[position] = a_list[position - 1]
position = position - 1
a_list[position] = current_value
def insertion_sort_binarysearch(a_list):
for index in range(1, len(a_list)):
current_value = a_list[index]
position = index
low=0
high=index-1
while low<=high:
mid=(low+high)/2
if a_list[mid]>current_value:
high=mid-1
else:
low=mid+1
while position > low:
a_list[position] = a_list[position - 1]
position = position -1
a_list[position] = current_value
a_list = [54, 26, 93, 15, 77, 31, 44, 55, 20]
insertion_sort(a_list)
print(a_list)
insertion_sort_binarysearch(a_list)
print(a_list)
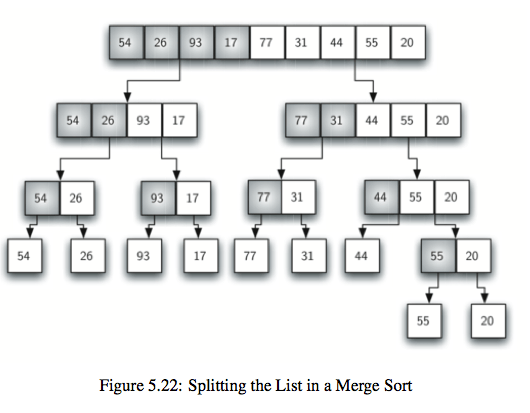
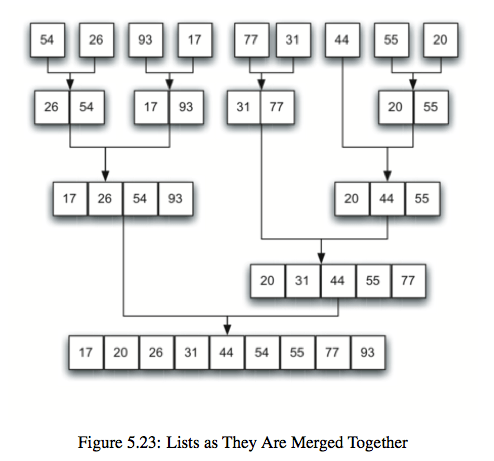
4.合并排序(merge sort):典型的是二路合并排序,将原始数据集分成两部分(不一定能够均分),分别对它们进行排序,然后将排序后的子数据集进行合并,这是典型的分治法策略。时间复杂度$O(nlogn)$
def merge_sort(a_list):
print("Splitting ", a_list)
if len(a_list) > 1:
mid = len(a_list) // 2
left_half = a_list[:mid]
right_half = a_list[mid:]
merge_sort(left_half)
merge_sort(right_half)
i=0;j=0;k=0;
while i < len(left_half) and j < len(right_half):
if left_half[i] < right_half[j]:
a_list[k] = left_half[i]
i=i+1
else:
a_list[k] = right_half[j]
j=j+1
k=k+1
while i < len(left_half):
a_list[k] = left_half[i]
i=i+1
k=k+1
while j < len(right_half):
a_list[k] = right_half[j]
j=j+1
k=k+1
print("Merging ", a_list)
a_list = [54, 26, 93, 17, 77, 31, 44, 55, 20]
merge_sort(a_list)
print(a_list)
算法导论2-4题利用合并排序可以在$O(nlogn)$的最坏情况下得到包含n个元素的数组的逆序对的数目。
[下面使用的是C++来实现的,合并排序的代码格式类似算法导论]
#include <iostream>
using namespace std;
int calculateInversions(int arr[], int p, int r);
int mergeInversions(int arr[], int p, int q, int r);
int main(int argc, const char * argv[])
{
int arr[] = {2,3,8,6,1};
int count = calculateInversions(arr, 0, 4);
cout << "count inversions : " << count << endl;
return 0;
}
int calculateInversions(int arr[], int p, int r) {
int count=0;
if(p < r) {
int q = (p + r) / 2;
count += calculateInversions(arr, p, q);
count += calculateInversions(arr, q+1, r);
count += mergeInversions(arr, p, q, r);
}
return count;
}
int mergeInversions(int arr[], int p, int q, int r){
int count=0;
int n1=q-p+1, n2=r-q;
int left[n1+1], right[n2+1];
for (int i=0; i<n1; i++) {
left[i]=arr[p+i];
}
for (int j=0; j<n2; j++) {
right[j]=arr[q+1+j];
}
left[n1]=INT32_MAX;
right[n2]=INT32_MAX;
int i=0, j=0;
for (int k=p; k<=r; k++) {
if (left[i]<=right[j]) {
arr[k]=left[i];
i++;
}else{
arr[k]=right[j];
count += n1-i;
j++;
}
}
return count;
}
5.快速排序(quick sort):
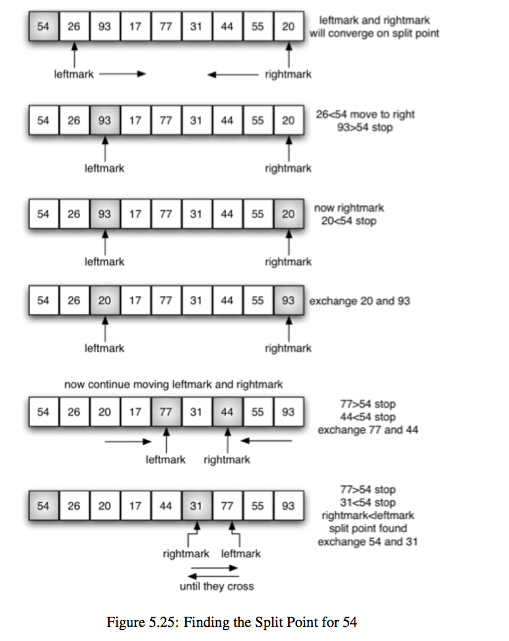
想法一:如下图所示,(它同样可以按照下面提到的算法导论中将数组分成了4个不同的部分,但是这里其实有更好的解释方法) 首先,它每次都是选择第一个元素都为主元,这个回合就是要确定主元的位置;然后,有两个指针,一个leftmark指向主元的后面一个位置,另一个rightmark指向要排序的数组最后一个元素;接着,两个指针分别向中间移动,leftmark遇到比主元大的元素停止,rightmark遇到比主元小的元素停止,如果此时leftmark<rightmark,也就是说中间还有未处理(未确定与主元大小关系)的元素,那么就交换leftmark和rightmark位置上的元素,然后重复刚才的移动操作,直到rightmark<leftmark;最后,停止移动时候rightmark就是主元要放置的位置,因为它停在一个比主元小的元素的位置上,之后交换主元和rightmark指向的元素即可。完了之后,递归地对主元左右两边的数组进行排序即可。
def quick_sort(a_list):
quick_sort_helper(a_list, 0, len(a_list) - 1)
def quick_sort_helper(a_list, first, last):
if first < last:
split_point = partition(a_list, first, last)
quick_sort_helper(a_list, first, split_point - 1)
quick_sort_helper(a_list, split_point + 1, last)
def partition(a_list, first, last):
pivot_value = a_list[first]
left_mark = first + 1
right_mark = last
done = False
while not done:
while left_mark <= right_mark and a_list[left_mark] <= pivot_value:
left_mark = left_mark + 1
while a_list[right_mark] >= pivot_value and right_mark >= left_mark:
right_mark = right_mark - 1
if right_mark < left_mark:
done = True
else:
temp = a_list[left_mark]
a_list[left_mark] = a_list[right_mark]
a_list[right_mark] = temp
temp = a_list[first]
a_list[first] = a_list[right_mark]
a_list[right_mark] = temp
return right_mark
a_list = [54, 26, 93, 17, 77, 31, 44, 55, 20]
quick_sort(a_list)
print(a_list)
想法二:(摘自算法导论)如下图所示,它选择最后的那个元素作为主元,它的思路是将数组划分成4部分:
第一部分:$p \le k \le i, A[k] \le pivot$
第二部分:$i+1 \le k \le j-1, A[k] \gt pivot$
第三部分:$j \le k \le r-1, A[k]$可以取任何值(因为它们还没有进行处理)
第四部分:$p \le k \le i, A[k] = pivot$
首先,让i指向要排序的数组的第一个元素的前面,p和j都指向第一个元素;然后,一直移动j直到主元前一个位置,一旦发现一个小于主元的元素就让i指向它的下一个位置,然后交换i和j对应位置上的元素。这样一定是可行的,因为i一直都是指向已发现的小于主元的元素中的最后一个,从i+1开始就大于主元了(或者还未确定/未处理),而j一直都是指向大于主元的元素中最后一个的后面一个位置,所以i+1和j位置上的元素交换就可以使得j发现的这个小于主元的元素移动到第一部分,而i+1位置上大于主元的元素移动到j的位置上,即第二部分的最后一个位置上。

根据算法导论中的伪代码的C++版本实现
#include <iostream>
using namespace std;
// partition, locate the pivot value in properate position
int partition(int a[], int low, int high){
int key = a[high];//pivot
int i=low-1, temp;
for (int j=low; j<high; j++) {
if (a[j]<key) {
i++;
temp = a[j];
a[j]=a[i];
a[i]=temp;
}
}
temp = a[high];
a[high] = a[i+1];
a[i+1] = temp;//i+1 is the split point
return i+1;
}
// quick sort
void quicksort(int a[], int low, int high) {
if (low < high) {
int p = partition(a,low,high);
quicksort(a, low, p-1);
quicksort(a, p+1, high);
}
}
// print array
void print(int a[],int len){
for (int i=0; i<len; i++) {
cout << a[i] << " ";
}
cout << endl;
}
int main(int argc, const char * argv[])
{
int a[]={3,5,2,7,9,10,33,28,19,6,8};
quicksort(a, 0, 10);
print(a,11);
}
由于快排每次都能够确定一个元素在数组中最终的位置,所以可以用快排来解决很多变种问题,例如在线性时间内求中位数或者其他顺序统计量的问题(例如第k大或者第k小的元素),该部分内容可以参考来自博客园
关于快排的性能分析可以参考来自博客园,一般来说划分之后两边越均衡的话快排的性能更好。为了避免最坏的情况出现(原始的数组是已经是有序的)可以使用随机化版本的快排。
另外,为了减少快排调用的栈深度可以使用模拟尾递归技术,通过对快排的修改可以保证最坏情况下栈深度为O(nlgn),该内容可以参见算法导论习题7-4。
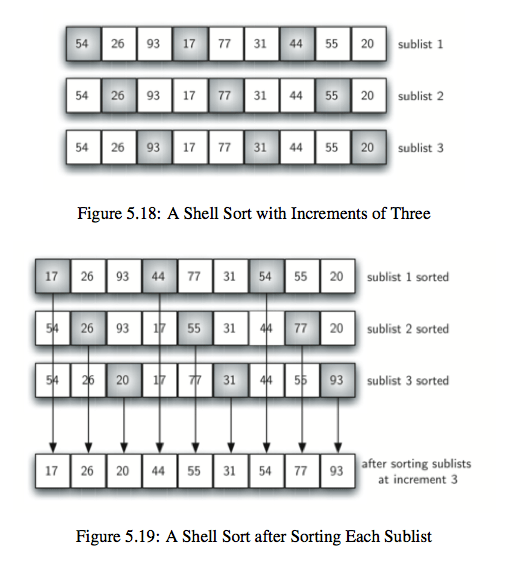
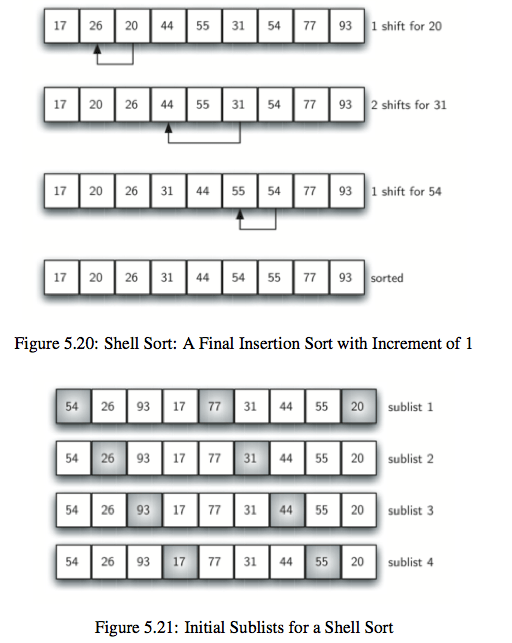
6.希尔排序:类似合并排序和插入排序的结合体,二路合并排序将原来的数组分成左右两部分,希尔排序则将数组按照一定的间隔分成几部分,每部分采用插入排序来排序,有意思的是这样做了之后,元素很多情况下就差不多在它应该呆的位置,所以效率不一定比插入排序差。时间复杂度为$[O(n),O(n^2)]$。
def shell_sort(a_list):
#how many sublists, also how many elements in a sublist
sublist_count = len(a_list) // 2
while sublist_count > 0:
for start_position in range(sublist_count):
gap_insertion_sort(a_list, start_position, sublist_count)
print("After increments of size", sublist_count, "The list is", a_list)
sublist_count = sublist_count // 2
def gap_insertion_sort(a_list, start, gap):
#start+gap is the second element in this sublist
for i in range(start + gap, len(a_list), gap):
current_value = a_list[i]
position = i
while position >= gap and a_list[position - gap] > current_value:
a_list[position] = a_list[position - gap] #move backward
position = position - gap
a_list[position] = current_value
a_list = [54, 26, 93, 17, 77, 31, 44, 55, 20, 88]
shell_sort(a_list)
print(a_list)
7.堆排序请参见该系列文章中的DataStrctures章节中的二叉堆部分的内容。
8.其他线性排序可以参见算法导论第8章或者看下这篇不错的文章
其实看个图就明白了,图摘自上面的博客,版权归原作者,谢谢!
计数排序:在数的范围很小时还是不错的,当数的范围很大的时候就不适用了,计数排序一般用于基数排序中。需要注意的是,计数完了之后进行插入时,为了保证排序的稳定性,需要从后往前插入。
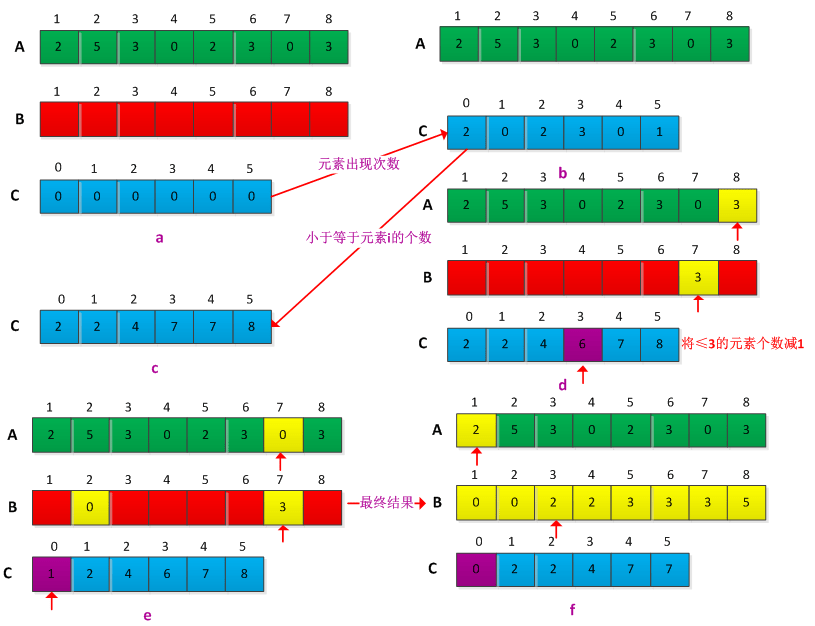
下面是计数排序的python实现,摘自Python Algorithms: Mastering Basic Algorithms in the Python Language
from collections import defaultdict
def counting_sort(A, key=lambda x: x):
B, C = [], defaultdict(list) # Output and "counts"
for x in A:
C[key(x)].append(x) # "Count" key(x)
for k in range(min(C), max(C) + 1): # For every key in the range
B.extend(C[k]) # Add values in sorted order
return B
seq = [randrange(100) for i in range(10)]
seq = counting_sort(seq)
基数排序:因为每位上的数字范围一般都是有限的,所以常配合使用计数排序对每位进行排序。
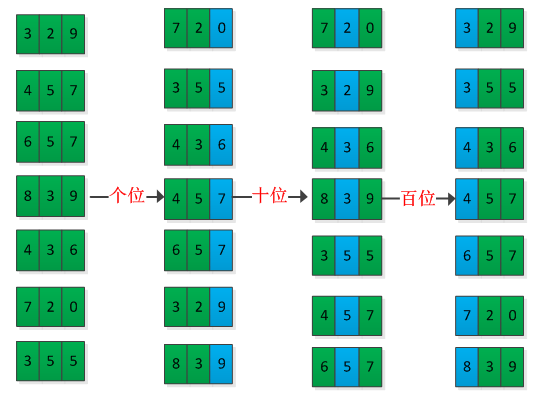
桶排序:适用于元素是均匀分布的,在每个桶内采用插入排序。
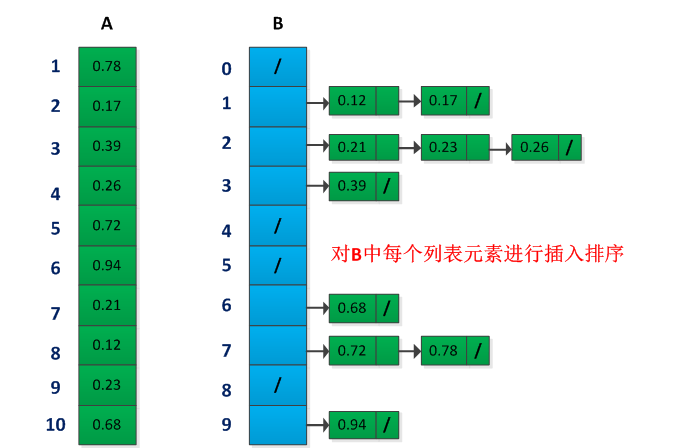
本节只是对各种排序进行一个介绍然后用python实现而已,更加详细地解释各种排序的内部思想的内容可以参见后面的Python算法设计篇之Induction&Recursion&Reduction