Python数据结构篇(1) 搜索
参考内容:
1.Problem Solving with Python
Chapter5: Search and Sorting online_link
2.算法导论
搜索(或查找)总结
(1)顺序查找:O(n)
(2)二分查找:O(lgn)
(3)Hash查找:O(1)
概念:hash,hash table,hash function 哈希表_on_wiki

常用的哈希函数:
1.reminder method:取余数(size=11,下图对11取余数,例如17取余数得到6)

2.folding method: 分组求和再取余数

3.mid-square method:平方值的中间两位数取余数

4.对于由字符的元素可以尝试使用ord函数来将字符串转换成一个有序的数值序列。在Python中ord函数可以得到对应字符的ASCII码值。将所有字符的码值累加再取余数。

但是,对于通过回文构词法构成的字符串它们得到的值总是一样,为了解决这个问题,可以根据字符的位置添加一个权重。
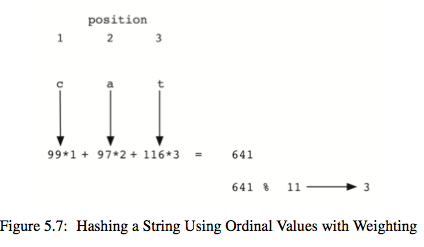
From wiki

使用哈希查找,难免遇到冲突,该如何解决冲突(Collision Resolution)呢?
常用的解决冲突的办法:
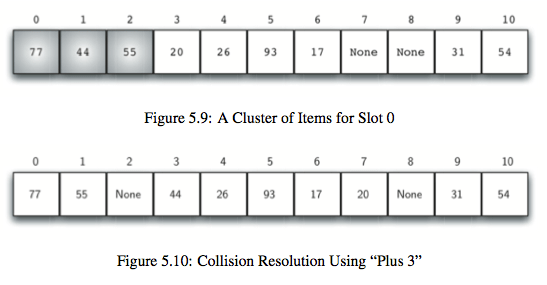
1.open address(开放寻址):线性探测(linear probing)下一个位置,缺点是容易造成聚集现象(cluster),解决聚集现象的办法是跳跃式地查找下一个空槽。数值的顺序:(54, 26, 93, 17, 77, 31, 44, 55, 20).
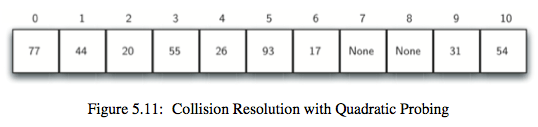
2.quadratic probing(平方探测):一开始的hash值为h,如果不是空槽,那就尝试h+1,还不是空槽就尝试h+4,依次继续尝试h+9,h+16等等。
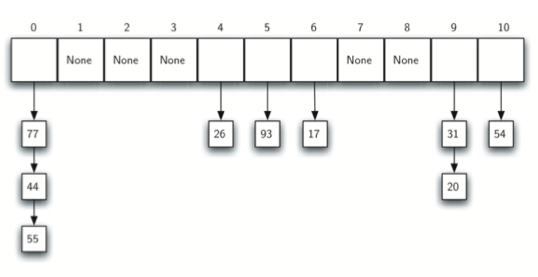
3.chain:利用链表链接起来
From wiki
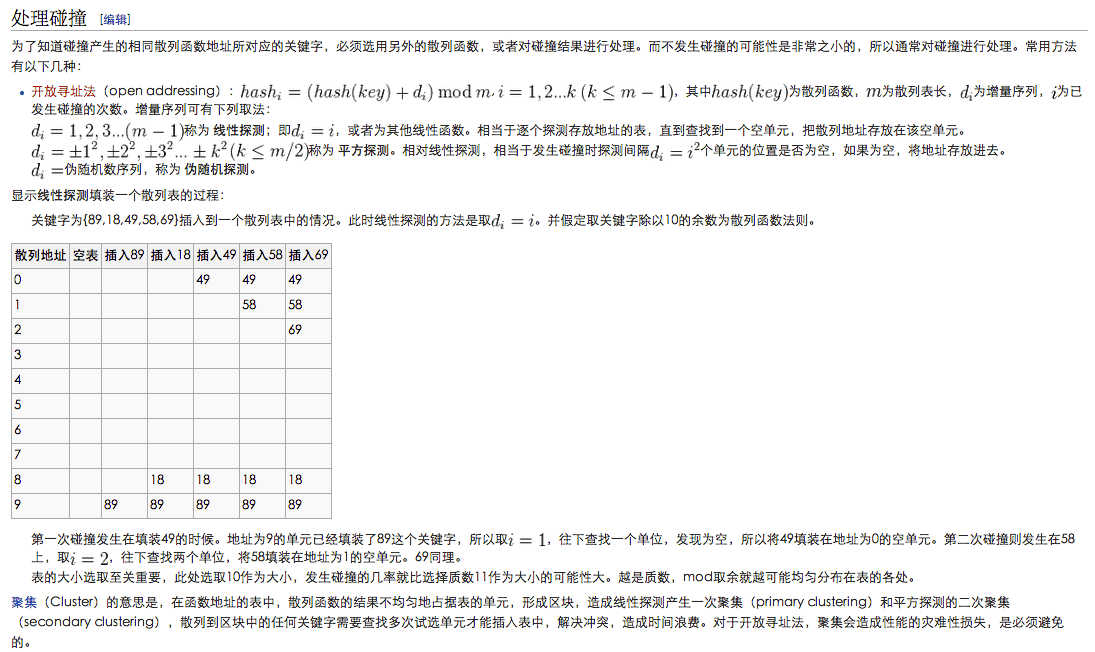
分析hash查找的性能:一般使用平均查找长度来衡量,和装载因子有关
散列表的载荷因子定义为:$\alpha$ = 填入表中的元素个数 / 散列表的长度
$\alpha$是散列表装满程度的标志因子。由于表长是定值,$\alpha$与“填入表中的元素个数”成正比,所以,$\alpha$越大,表明填入表中的元素越多,产生冲突的可能性就越大;反之,$\alpha$越小,标明填入表中的元素越少,产生冲突的可能性就越小。实际上,散列表的平均查找长度是载荷因子$\alpha$的函数,只是不同处理冲突的方法有不同的函数。
对于开放定址法,荷载因子是特别重要因素,应严格限制在0.7-0.8以下。超过0.8,查表时的CPU缓存不命中(cache missing)按照指数曲线上升。因此,一些采用开放定址法的hash库,如Java的系统库限制了荷载因子为0.75,超过此值将resize散列表。

From wiki

下面的代码包含了顺序查找,二分查找,哈希查找(size=11, plus 1, reminder method)
def sequential_search(a_list, item):
pos = 0
found = False
while pos < len(a_list) and not found:
if a_list[pos] == item:
found = True
else:
pos = pos+1
return found
test_list = [1, 2, 32, 8, 17, 19, 42, 13, 0]
print(sequential_search(test_list, 3))
print(sequential_search(test_list, 13))
def binary_search(a_list, item):
first = 0
last = len(a_list) - 1
found = False
while first <= last and not found:
midpoint = (first + last) // 2
if a_list[midpoint] == item:
found = True
else:
if item < a_list[midpoint]:
last = midpoint - 1
else:
first = midpoint + 1
return found
test_list = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binary_search(test_list, 3))
print(binary_search(test_list, 13))
class HashTable:
def __init__(self):
self.size = 11
self.slots = [None] * self.size
self.data = [None] * self.size
#put data in slot
def put_data_in_slot(self,key,data,slot):
if self.slots[slot] == None: # '==None' ? or 'is None' ?
self.slots[slot] = key
self.data[slot] = data
return True
else:
if self.slots[slot] == key: # not None
self.data[slot] = data #replace
return True
else:
return False
def put(self, key, data):
slot = self.hash_function(key, self.size);
result = self.put_data_in_slot(key,data,slot);
while not result:
slot = self.rehash(slot, self.size);
result=self.put_data_in_slot(key,data,slot);
#reminder method
def hash_function(self, key, size):
return key % size
#plus 1
def rehash(self, old_hash, size):
return (old_hash + 1) % size
def get(self, key):
start_slot = self.hash_function(key, len(self.slots))
data = None
stop = False
found = False
position = start_slot
while self.slots[position] != None and not found and not stop:
if self.slots[position] == key:
found = True
data = self.data[position]
else:
position=self.rehash(position, len(self.slots))
if position == start_slot:
stop = True
return data
def __getitem__(self, key):
return self.get(key)
def __setitem__(self, key, data):
self.put(key, data)
if __name__ == '__main__':
table=HashTable();
table[54]='cat';
table[26]='dog';
table[93]='lion';
table[17]="tiger";
table[77]="bird";
table[44]="goat";
table[55]="pig";
table[20]="chicken";
print table.slots;
print table.data;
# [77, 44, 55, None, 26, 93, 17, None, None, 20, 54]
# ['bird', 'goat', 'pig', None, 'dog', 'lion', 'tiger', None, None, 'chicken', 'cat']